前言

最近遇到了怪物在ai寻路的目标点为同一个的时候，会出现相互挤压的情况。所以开始研究群体避障算法。这片文章主要讲一下最基础的VO（Velocity Obstacle）算法。

正文

其实vo算法不是很难的，就是你得实时算它前面是不是会碰到物体，因为是简单的，所以单个物体只管自己的。我先晒一张经典的图

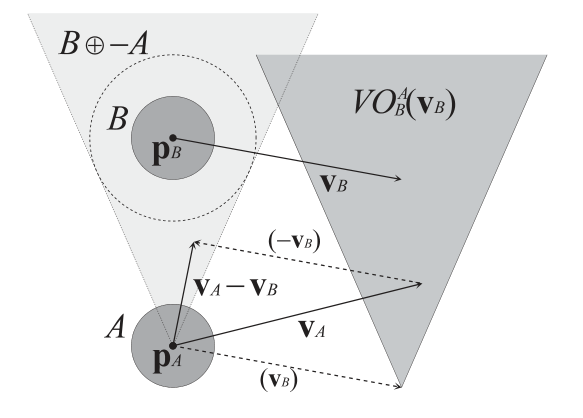
这张图在所以讲vo算法的文章里都会出现的，它直观的展示了vo是怎么算物品之间的碰撞。现在我就基于这个图来详细讲解下相关的知识点。

闵可夫斯基和

在这张图里我们会看到B里有一个实体圈，和一个虚线圈。然后你会发现生成的B⨁−A这个三角形实际上是从A的中心点PA为起点画的，所以可以理解那个虚拟的B圈实际上是把A圈给叠加上了。这里涉及到了一个集合知识点就是闵可夫斯基和（闵氏和）。
概念：两个图形A，B的闵氏和C={a+b|a∈A,b∈B}
其实就是从原点向着图形A内部的每一个点做向量，将图形B沿每个向量移动，最终位置的并集就是闵氏和。
我们来看一个图片吧

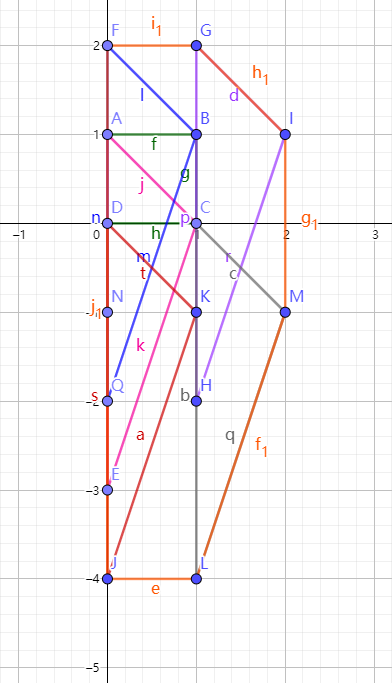
在这张图里a（A,B,C,D）b(A,C,E)。现在我们用它做一个闵氏和，先把b往DA向量方向移动，得到了一个（F,B,Q）这个图型，其他的向量也按这样的移动，我们最后就会得到一个并集成（F,G,I,M,L,J）这个图型。这个图形就是我们要算的a和b的闵氏和。
结合这个知识点，我们现在来看VO的那张图我们就很容易理解了，把B和A放在同一个圆心上，然后沿着圆的四周往外扩散A的半径向量。得到虚框B。

相对位移

当我们A沿着VA移动，B沿着VB移动的时候，我们要确定两个图形是否会碰撞到，因为我们是从a画的一个扇形，所以我们需要计算下A的相对于B的移动向量，这个就用向量相减就好了。算出一个VA-VB的向量，然后我们PA质点沿着VA-VB的方向画一个和B虚框相切的一个图形B⨁−A。因为实际计算不是求的相对速度，是VA的实际速度，所以我们需要加上VB。这样我们就得到了一个深色的三角形。

结论

当我们的速度不属于这个深色三角形内的时候，他们就不会发生碰撞。

补充

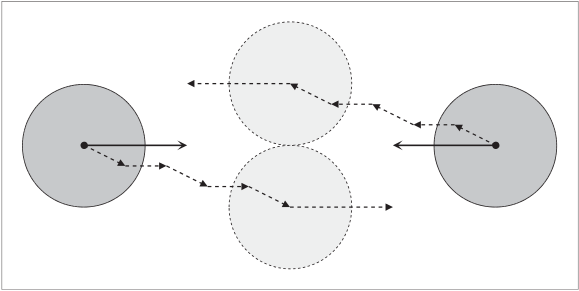
因为VO是把对象都当成一个独立的个体，所以它在计算的时候是实时计算的，当两个物体独立计算的时候，所以他们会单独计算自己的避障速度方向，当A，B沿着避障方向移动的时候，他们在下一次计算会发现自己不在对方的碰撞区域内，所以会修改方向沿着之前会碰撞的方向移动，再下一次计算的时候发现自己又在碰撞区域内了，又开始偏移移动，这样往复以后，就会出现抖动。后面我研究研究VO的优化算法，再讲解下怎么解决这个问题。

概念

使用的思想是分治思想。把需要排序的数组中重建分成两部分，然后前后两部分分别排序，需要一直分解下去，直到能两个值相互比较。然后再将排序好的两个部分合并在一起。

合并

我们需要申请一个临时数组，这个数组的大小和我们排序的两个组的大小之和一样。然后我们用两个下标i，j，来标识我们当前读到的是两个组的第几个位置，然后这两个下标的值来做比较，但一个值满足要求的时候，我们就把这个值放在临时数组里，然后这个下标后移一位，继续比较。当任意一个下标到达那个组的最后一位的时候，我们就不需要做比较了，直接把另外一组剩下的放在临时数组的最后。

void merge_sort_c(int [] a,int p,int r)
            {
                if (p >= r)
                    return;
                int q = (p + r) / 2;
                merge_sort_c(a,p, q);
                merge_sort_c(a, q + 1, r);
                merage(a, p, q, r);
            }
            void merage(int[]a,int p,int q,int r)
            {
                int i = p;
                int j = q+1;
                int k = 0;
                int[] temp = new int[r - p+1];
                while (i <= q && j <= r)
                {
                    if (a[i] <= a[j])
                    {
                        temp[k++] = a[i++];
                    }
                    else
                    {
                        temp[k++] = a[j++];
                    }
                }
                int start = i;
                int end = q;
                if (j <= r)
                {
                    start = j;
                    end = r;
                }
                while (start <= end)
                {
                    temp[k++] = a[start++];
                }
                for(int ii = 0; ii < r - p+1; ii++)
                {
                    a[p + ii] = temp[ii];
                }
            }

1. 当我们把第二组的多出来的数据整体放在第一组后面，那归并排序是稳定排序

2. 归并排序的时间复杂度o(nlogn）

3. 归并排序的空间复杂度不是原地排序，因为在合并的时候需要临时空间。o(n)

概念

也分为未排序区和排序区。但是选择排序每次都从未排序中找到我们要的元素放在排序区的最后。

int[] t = new int[10] { 43, 23, 432, 5, 2, 6, 43, 2, 67, 4 };
                for(int i = 0; i < t.Length; i++)
                {
                    int v = t[i];
                    int index = i;
                    for (int j = t.Length-1; j > i; --j)
                    {
                        if (v > t[j])
                        {
                            index = j;
                            v = t[j];
                        }
                    }
                    t[index] = t[i];
                    t[i] = v;
                }
                for(int i = 0; i < t.Length; i++)
                {
                    Console.WriteLine("{0}={1}", i, t[i]);
                }

1. 因为只会交换一次我们找到满足条件的数据放在已排序的最后，所以这个排序的空间复杂度为o(1),是原地排序算法

2. 这个排序不是稳定排序算法，因为每次都会去找剩下满足的元素和前面的元素进行交换

3. 最坏，最好，和平均时间复杂度都是o(n*n).

概念

插入排序就是把数组分为两个区间，一个是有序区间，一个是未排序区间。初始的时候有序区间就只有一个元素，那就是数组的第一个元素，然后取未排序区间中的元素往有序区间中插进去，一直等到未排序区间中的所有元素为空。

int[] t = new int[10] { 54, 23, 43, 2, 3, 5, 1, 2, 6, 7 };
                for (int i = 0; i < t.Length; i++)
                {
                    int v = t[i];
                    int j = i - 1;
                    for (; j > 0; --j)
                    {
                        if (v > t[j])
                        {
                            t[j + 1] = t[j];
                        }
                        else
                        {
                            break;
                        }
                    }
                }
                for(int i = 0; i < t.Length; i++)
                {
                    Console.WriteLine("{0}={1}", i, t[i]);
                }

1. 插入排序算法不需要额外的空间，所以它的空间复杂度为o(1),是原地排序算法。

2. 插入的时候只是插到它所需要的位置，不会修改它后面位置的顺序，所以是稳定排序算法。

3. 最好情况下，我们要排序的数据是有序的，所以我们只需要做o(n)的时间复杂度。最坏的情况下，我们要排序的数据是逆序的，所以我们要做o(nn)的时间复杂度。在数组中插入一个数据的时间平均时间复杂度是o(n)，我们需要执行n次操作，所以平均时间复杂度是o(nn)。

概念

每次冒泡就是相邻的两个数进行比较，如果两个数据的关系不满足我们所要求的的，那我们就进行交换。一次冒泡操作至少会让一个元素移动到它所应该在的位置。

int[] t = new int[10] { 2, 3, 4, 2, 43, 54, 23, 43, 1, 67};
for(int i = 0; i < t.Length; i++)
    {
      for(int j = 0; j < t.Length-i-1; j++)
          {
              if (t[j+1] > t[j])
                 {
                   int temp = t[j+1];
                   t[j+1] = t[j];
                   t[j] = temp;
                  }
            }
     }
     for(int i = 0; i < t.Length; i++)
        {
          Console.WriteLine("{0}={1}", i, t[i]);
        }

1. 因为只涉及到相邻的两个数的操作，所以它的空间复杂度是o(1）是原地算法排序。

2. 因为只有当相邻的两个元素不一致的时候我们才会去交换两个元素的位置，所以这个排序也是一个稳定排序算法。

3. 在最好的情况下就是说他们已经是有序的情况下他们的时间复杂度是o(n),在最坏的情况下就是说它们是反倒序的情况下，它的时间复杂度是o（nn）；还有一种叫平均时间复杂度n(n-1)/4，一般来说我们就看做o(n*n)。

排序算法的执行效率

1. 最好情况，最坏情况，平均情况时间复杂度
   第一，有些算法会区分，为了好对比，我们最好都要做一下区分。
   第二，对于要排序的数据，有的接近有序，有的是完全无序的。有序度的不同，对于排序的执行时间肯定有影响的。

2. 时间复杂度的系数，常数，低阶
   时间复杂度一般都是数据规模n很大的时候的一个增长趋势，所以在这个时候它就会忽略系数，常数，低阶。但是我们一般排序的数据规模10，100，1000，这样很小的规模的数，所以我们要考虑系数，常数，低阶。

3. 比较次数和交换（或移动）次数
   基本比较的排序算法，会设计两种操作。一种是比较两个数的大小，一种是交换两个数的位置。所以我们在分析排序算法的时候这两个都要考虑。

排序算法的内存消耗

算法的内存消耗可以通过空间复杂度来衡量，但是针对排序算法的时候，我们新加了一个概念，原地排序。原地排序就是特指空间复杂度为o(1）的排序算法

排序稳定性

针对排序算法还有一个很重要的指标，就是稳定性。这个概念就是说待排序的元素中有值相等的元素，在排序之后相等元素的先后顺序不会发生改变
发生改变的排序算法叫不稳定排序算法
不发生改变的排序算法叫稳定排序算法
为什么排序的稳定性比较重要呢？一般来说我们实际使用的时候，很有可能对一组数据做两次排序。如果排序算法不稳定的话，那我们第二次排序就会覆盖掉第一次排序所产生我们需要的结果。

原理

中心思想是用了二分法，首先取一个标致值，用这个标致值来分割两部分，一部分比它大，一部分比它小，然后就这样递归下去，直到全部的值都已经变成有序的。

上图

用图的方式更方便理解这个概念。

代码详情

第一种

 void Quicksort(int[]numbers,int left,int right)
            {
                if (left < right)
                {
                    int middle = numbers[(left + right) / 2];
                    int i = left -1 ;
                    int j = right + 1;
                    while (true)
                    {
                        while (numbers[++i] < middle) ;
                        while (numbers[--j] > middle) ;
                        if (i >= j)
                            break;
                        swap(numbers, i, j);
                    }
                    Quicksort(numbers, left, i - 1);
                    Quicksort(numbers, j+1, right);
                }
            }
void swap (int[]numbers,int i,int j)
            {
                int number = numbers[i];
                numbers[i] = numbers[j];
                numbers[j] = number;
            }

代码解释

首先我们找到一个标识值middle这个值是我们要分隔数组的中间值，然后我们定义两个下标，分别代表，比middle大的值，和比middle小的值，分别用i，j来表示，然后我们在while循环中，首先找到比middlle大的i下标的值，和比middle小的j下标的值，来调换位置，当找到i已经比j大等的时候，说明我们这次已经找完了，已经查到了middle这个值的下标，然后我们就开始分左右两个部分继续来大小划分。这时候的开始左边的区间就左边是这次的左区间加上这次找到的标识左边下标，右边区间就是标识右边的值加上当前区间的右边下标。

第二种

void Quicksort1(int [] numbers,int left,int right)
            {
                int i, last;
                if (left >= right)
                    return;
                swap(numbers, left, (left + right) / 2);
                last = left;
                for(i = left + 1; i < right; i++)
                {
                    if (numbers[i] < numbers[left])
                    {
                        swap(numbers, ++last, i);
                    }
                }
                swap(numbers, left, last);
                Quicksort1(numbers, left, last);
                Quicksort1(numbers, last+1, right);
            }
 void swap (int[]numbers,int i,int j)
            {
                int number = numbers[i];
                numbers[i] = numbers[j];
                numbers[j] = number;
            }

代码解释

首先我们把最左边的值和中间的值交换，然后我们记录下来交换的值的位置设置为last，因为我们已经把中间值和最左边的值交换了，所以我们标志值在最左边，我们就用这个值来和当前数组中的所有值来进行比较，如果比较的值比标识值小的话，就累加last然后交换，就把这个值换到了左边去了，如果大的话就不动，所以换过的左边都是比标识小的，最后当前的标识符换到最后一个最小的值的位置，那个位置之后就没有比标识值更小的了。然后再递归分割。