前言
我们在使用一些组件的时候,很容易在不了解它底层实现的情况下,使用出一些性能的问题。作为一个良好的程序员来说,能在在遇到这种问题的时候给出解决方案,算是一个基本的职业素质。所以我们需要在使用组件的时候知其所以然。
为什么需要了解List
List 这个组件是一个可伸缩的数组组件,我们会常常用它来代替数组,因为是可伸缩的,所以我们使用的地方太多了。
需要了解哪些东西
- 增加元素
- 删除元素
- 修改元素
- 怎么伸缩(这个其实在上面应该会说)
源码地址
正文
构造部分
首先我们来看下List的构造部分,源码如下:
public class List<T> : IList<T>,System.Collections.IList,IReadOnlyList<T>
{
private const int _DefaultCapacity = 4;
private T[] _items;
[ContractPublicPropertyName("Count")]
private int _size;
private int _version;
[NoSerialized]
private Object _syncRoot;
static readonly T[] _emptyArray = new T[0];
public List(){
_items = _emptyArray;
}
public List(int capacity){
if(capacity<0) ThrowHelper.ThrowArgumentOutOfRangeException(ExcptionArgument.capacity,ExceptionResource.ArgumentOutOfRange_NeedNonNegNum);
Contract.EndContractBlock();
if(capacity == 0)
_items = _emptyArray;
else
_items = new T[capacity];
}
public List(IEnumerable<T> collection){
if (collection==null)
ThrowHelper.ThrowArgumentNullException(ExceptionArgument.collection);
Contract.EndContractBlock();
ICollection<T> c = collection as ICollection<T>;
if( c != null) {
int count = c.Count;
if (count == 0)
{
_items = _emptyArray;
}
else {
_items = new T[count];
c.CopyTo(_items, 0);
_size = count;
}
}
else {
_size = 0;
_items = _emptyArray;
using(IEnumerator<T> en = collection.GetEnumerator()) {
while(en.MoveNext()) {
Add(en.Current);
}
}
}
//...
//其他内容
}
}
从源码中我们可以知道,List继承IList,和IReadOnlyList这两个接口,IList是提供主要的接口,IReadOnlyList提供了迭代接口。
我们还能知道List内部是用数组来实现的,它有三种构造方法,一个是啥都不传的,默认初始化一个长度0的数组,一个是初始化数组长度的构造函数,一个是复制给定集合内容的构造函数,长度和内容都和传进来的数组一样。
添加
当我们看到第三种构造函数的时候,我们会发现最下面有一个Add这个函数的调用,这个函数就是List中添加。
源码如下:
public void Add(T item){
if(_size == _item.Length) ExsureCapacity(_size + 1);
_item[_size++] = item;
_version++;
}
private void EnsureCapacity(int min){
if(_item.Length < min){
int newCapacity = _items.Length == 0 ? _defaultCapacity : _items.Length * 2;
if((uint)newCapacity > Array.MaxArrayLength) newCapacity = Array.MaxArrayLength;
if(newCapacity < min) newCapacity = min;
Capacity = newCapacity;
}
}
public int Capacity{
get{
Contract.Ensures(Contract.Result<int>() >= 0);
return _item.Length;
}
set{
if(value < _size){
ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.value, ExceptionResource.ArgumentOutOfRange_SmallCapacity);
}
Contract.EndContractBlock();
if(value != _items.Length){
if(value > 0){
T[] newItems = new T[value];
if(_size > 0){
Array.Copy(_items,0,newItems,0,_size);
}
_items = newItems;
}else{
_items = _emptyArray;
}
}
}
}
从上面的源码我们可以看出来,当List在Add一个item的时候,会先去判断这个数组是不是已经满了,如果满了就拓容,从4,16,32 ...n(上一次数组大小)*2 这样的大小来拓容的,当拓容之后,会新建一个新的数组,把原来数组内容给拷贝进去,然后再去添加新的元素。
-
如果你直接调用Capacity赋值数组商都为负数的时候,你会出现数组被清理成默认的,但是数组的标记size(这个代表当前添加到数组第几个位置)却没有清空,下一次你要用的时候,会浪费之前那么多的内存空间。
-
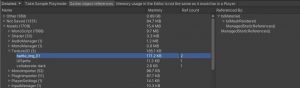
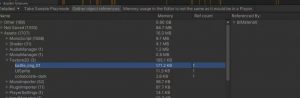
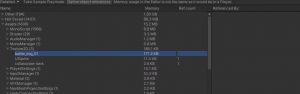
当你在添加一堆数据的时候(例如128个数据)在一开始没有给List赋值长度的话,它就会在你添加的时候进行六次扩容,然后这六次扩容中有五次是需要拷贝元素数据的,这样每次拷贝都会造成新的内存垃圾,这样就会给GC带来很多负担。
-
如果添加的数量不得当,也会照成内存空间的浪费,比如元素数量为520的时候,List就会扩容到1024个元素,这样就会多出502个空间单位没有被使用。
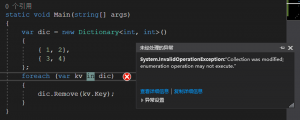
删除
删除我们主要看Remove这个函数
源码如下:
public bool Remove(T item){
int index = indexOf(item);
if (index>=0){
RemoveAt(index);
return true;
}
return false;
}
public int indexof(T item){
Contract.Ensures(Contract.Result<int>() >= -1);
Contract.Ensures(Contract.Result<int>() < Count);
return Array.IndexOf(_items,item,0,_size);
}
public void RemoveAt(int index){
if((uint)index >= (uint)_size){
ThrowHelper.ThrowArgumentOutOfRangeException();
}
Contract.EndContractBlock();
_size--;
if(index < _size){
Array.Copy(_items,index+1,_items,index,_size-index);
}
_item[size] = default(T);
_version++;
}
Remove接口中包含了IndexOf和RemoveAt,这两个方法,IndexOf是为了定位要删除的元素的位置,这个接口的实现是按索引从0到n个位置做意义比较,时间复杂度为O(n);RemoveAt这个方法是用来删除指定位置的元素,但是它的实现是用Array.Copy来进行数组的覆盖。
插入
源码如下:
public void Insert(int index,T item){
if((uint) index > (uint)_size){
ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.index, ExceptionResource.ArgumentOutOfRange_ListInsert);
}
Contract.EndContractBlock();
if(_size == _items.Length) EnsureCapacity(_size + 1);
if(index < _size){
Array.Copy(_items,index,_items,index+1,_size-index);
}
_items[index] = item;
_size++;
_version++;
}
从源码中我们可以看到,Insert和Add接口一样,都会先检查容量是否足够,如果不够就扩容,插入的位置是否是数组的最后,如果不是进行数组拷贝,将index后面的元素集体后移一位。
在这里我们可以很清楚一个概念,就是最坏的情况下,我们插入一个数据需要做2次数据拷贝,会造成GC时的压力。
思考
其他相关的接口比如AddRange,RemoveRange,InsertRange的原理其实和Add,Remove,Insert一样,区别就是从单个元素变成以容易为单位的操作,都是做一些重复覆盖的操作,和扩容。他们没有进行任何形式的优化,都是使用顺序迭代的方式。如果频繁调用,会照成不小的内存冗余和GC的压力。
其他的一些接口说明
比如[]的实现
public T this[int index] {
get {
// Following trick can reduce the range check by one
if ((uint) index >= (uint)_size) {
ThrowHelper.ThrowArgumentOutOfRangeException();
}
Contract.EndContractBlock();
return _items[index];
}
set {
if ((uint) index >= (uint)_size) {
ThrowHelper.ThrowArgumentOutOfRangeException();
}
Contract.EndContractBlock();
_items[index] = value;
_version++;
}
}
这个就是直接使用数组的的索引方式来获取元素,赋值元素,
Clear清除接口
public void Clear() {
if (_size > 0)
{
Array.Clear(_items, 0, _size); // Don't need to doc this but we clear the elements so that the gc can reclaim the references.
_size = 0;
}
_version++;
}
调用的时候不会去删除数组内的元素,只是将元素清零,然后设置_size为0;
Contains接口
public bool Contains(T item) {
if ((Object) item == null) {
for(int i=0; i<_size; i++)
if ((Object) _items[i] == null)
return true;
return false;
}
else {
EqualityComparer<T> c = EqualityComparer<T>.Default;
for(int i=0; i<_size; i++) {
if (c.Equals(_items[i], item)) return true;
}
return false;
}
}
我们看到它就是做了一次线性比较的方式来对数组进行迭代查找,并且返回的是第一个比对上的元素。
ToArray接口
public T[] ToArray() {
Contract.Ensures(Contract.Result<T[]>() != null);
Contract.Ensures(Contract.Result<T[]>().Length == Count);
T[] array = new T[_size];
Array.Copy(_items, 0, array, 0, _size);
return array;
}
它的实现就是新建一个数组,然后把元素拷贝进去再返回出来。
Find 接口
public T Find(Predicate<T> match) {
if( match == null) {
ThrowHelper.ThrowArgumentNullException(ExceptionArgument.match);
}
Contract.EndContractBlock();
for(int i = 0 ; i < _size; i++) {
if(match(_items[i])) {
return _items[i];
}
}
return default(T);
}
同样适用的是线性查找,对每个元素都进行比较,时间复杂度为O(n).
Enumerator 迭代的实现
public Enumerator GetEnumerator() {
return new Enumerator(this);
}
IEnumerator<T> IEnumerable<T>.GetEnumerator() {
return new Enumerator(this);
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator() {
return new Enumerator(this);
}
public struct Enumerator : IEnumerator<T>, System.Collections.IEnumerator
{
private List<T> list;
private int index;
private int version;
private T current;
internal Enumerator(List<T> list) {
this.list = list;
index = 0;
version = list._version;
current = default(T);
}
public void Dispose() {
}
public bool MoveNext() {
List<T> localList = list;
if (version == localList._version && ((uint)index < (uint)localList._size))
{
current = localList._items[index];
index++;
return true;
}
return MoveNextRare();
}
private bool MoveNextRare()
{
if (version != list._version) {
ThrowHelper.ThrowInvalidOperationException(ExceptionResource.InvalidOperation_EnumFailedVersion);
}
index = list._size + 1;
current = default(T);
return false;
}
public T Current {
get {
return current;
}
}
Object System.Collections.IEnumerator.Current {
get {
if( index == 0 || index == list._size + 1) {
ThrowHelper.ThrowInvalidOperationException(ExceptionResource.InvalidOperation_EnumOpCantHappen);
}
return Current;
}
}
void System.Collections.IEnumerator.Reset() {
if (version != list._version) {
ThrowHelper.ThrowInvalidOperationException(ExceptionResource.InvalidOperation_EnumFailedVersion);
}
index = 0;
current = default(T);
}
}
我们可以看到Enumerator这个接口在每次被获取的时候都是new出来的,如果使用大量的迭代器的时候就会有大量的对象,照成GC压力
Sort接口
public void Sort()
{
Sort(0, Count, null);
}
public void Sort(IComparer<T> comparer)
{
Sort(0, Count, comparer);
}
public void Sort(int index, int count, IComparer<T> comparer) {
if (index < 0) {
ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.index, ExceptionResource.ArgumentOutOfRange_NeedNonNegNum);
}
if (count < 0) {
ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.count, ExceptionResource.ArgumentOutOfRange_NeedNonNegNum);
}
if (_size - index < count)
ThrowHelper.ThrowArgumentException(ExceptionResource.Argument_InvalidOffLen);
Contract.EndContractBlock();
Array.Sort<T>(_items, index, count, comparer);
_version++;
}
public void Sort(Comparison<T> comparison) {
if( comparison == null) {
ThrowHelper.ThrowArgumentNullException(ExceptionArgument.match);
}
Contract.EndContractBlock();
if( _size > 0) {
IComparer<T> comparer = new Array.FunctorComparer<T>(comparison);
Array.Sort(_items, 0, _size, comparer);
}
}
// Array.Sort
internal void Sort(int left, int length)
{
#if FEATURE_CORECLR
// Since QuickSort and IntrospectiveSort produce different sorting sequence for equal keys the upgrade
// to IntrospectiveSort was quirked. However since the phone builds always shipped with the new sort aka
// IntrospectiveSort and we would want to continue using this sort moving forward CoreCLR always uses the new sort.
IntrospectiveSort(left, length);
#else
if (BinaryCompatibility.TargetsAtLeast_Desktop_V4_5)
{
IntrospectiveSort(left, length);
}
else
{
DepthLimitedQuickSort(left, length + left - 1, IntrospectiveSortUtilities.QuickSortDepthThreshold);
}
#endif
}
private void DepthLimitedQuickSort(int left, int right, int depthLimit)
{
// Can use the much faster jit helpers for array access.
do
{
if (depthLimit == 0)
{
// Add a try block here to detect IComparers (or their
// underlying IComparables, etc) that are bogus.
try
{
Heapsort(left, right);
return;
}
catch (IndexOutOfRangeException)
{
throw new ArgumentException(Environment.GetResourceString("Arg_BogusIComparer", comparer));
}
catch (Exception e)
{
throw new InvalidOperationException(Environment.GetResourceString("InvalidOperation_IComparerFailed"), e);
}
}
int i = left;
int j = right;
// pre-sort the low, middle (pivot), and high values in place.
// this improves performance in the face of already sorted data, or
// data that is made up of multiple sorted runs appended together.
int middle = GetMedian(i, j);
// Add a try block here to detect IComparers (or their
// underlying IComparables, etc) that are bogus.
try
{
SwapIfGreaterWithItems(i, middle); // swap the low with the mid point
SwapIfGreaterWithItems(i, j); // swap the low with the high
SwapIfGreaterWithItems(middle, j); // swap the middle with the high
}
catch (Exception e)
{
throw new InvalidOperationException(Environment.GetResourceString("InvalidOperation_IComparerFailed"), e);
}
Object x = keys[middle];
do
{
// Add a try block here to detect IComparers (or their
// underlying IComparables, etc) that are bogus.
try
{
while (comparer.Compare(keys[i], x) < 0) i++;
while (comparer.Compare(x, keys[j]) < 0) j--;
}
catch (IndexOutOfRangeException)
{
throw new ArgumentException(Environment.GetResourceString("Arg_BogusIComparer", comparer));
}
catch (Exception e)
{
throw new InvalidOperationException(Environment.GetResourceString("InvalidOperation_IComparerFailed"), e);
}
Contract.Assert(i >= left && j <= right, "(i>=left && j<=right) Sort failed - Is your IComparer bogus?");
if (i > j) break;
if (i < j)
{
Object key = keys[i];
keys[i] = keys[j];
keys[j] = key;
if (items != null)
{
Object item = items[i];
items[i] = items[j];
items[j] = item;
}
}
i++;
j--;
} while (i <= j);
// The next iteration of the while loop is to "recursively" sort the larger half of the array and the
// following calls recrusively sort the smaller half. So we subtrack one from depthLimit here so
// both sorts see the new value.
depthLimit--;
if (j - left <= right - i)
{
if (left < j) DepthLimitedQuickSort(left, j, depthLimit);
left = i;
}
else
{
if (i < right) DepthLimitedQuickSort(i, right, depthLimit);
right = j;
}
} while (left < right);
}
我们可以看到使用的排序方法是用的快排,所以它的时间复杂度为O(nlogn)
总结
在分析完之后,我们可以知道List的效率并不高,只是通用性强,方便而已,大部分的算法都是使用线性复杂度的算法,这种算法遇到规模比较大的计算量级的时候就会照成大量的CPU的消耗。而且它的内存分配方式极其的不合理,只要元素不断的增加就会多次new数组,然后抛弃原来的数组,造成GC压力。所以List是一个好用但不高效的组件。