引用原文 https://www.cnblogs.com/InCerry/p/10325290.html

前言

对于c#中的Dictionary类相信大家都不陌生，这是一个Collection（集合）类型，可以通过Key/Value（键值对）的形式来存放数据；改类最大的优点就是它查询元素的时间复杂度接近o(1),实际项目中常被用来做一些数据的本地缓存，提升整体效率。
那个是什么样的设计能让Dictionary类实现o（1）的时间复杂度呢？这就是这篇文章想和大家讨论的东西；这些都是个人的一些理解和观点。

理论知识

对于Dictionary的实现原理，有两个关键的算法，一个是hash算法，一个是用于对hash碰撞冲突解决算法。

1，hash算法

Hash算法是一种数字摘要算法，它能将不定长度的二进制数据集给映射到一个较短的二进制长度数据集，常见的MD5算法就是一种Hash算法，通过MD5算法可对任何数据生成数字摘要。而实现了Hash算法的函数我们叫它Hash函数。Hash函数又以下几点特征：

1. 相同的数据进行Hash运算，得到的结果一定相同。
HashFunc(key1) == HashFunc(key1);

2. 不同的数据进行Hash运算，其结果可能会相同（Hash会产生碰撞）.key1 != key2 => HashFunc(key1) == HashFunc(key2)

3. Hash运算时不可逆，不能由key获取原始的数据.key => HashFunc(key)但是HashFunc(key)=\=> key

散列函数还需要满足以下性质：

1. 从数据到整数值（0~N-1）的映射

2. 足够分散

3. 不易冲突

“足够分散”是指，即使数据只有很小的差异，散列函数的计算也需要很大的差异。
“不易冲突”是指，不易发生不同的数据得到相同的散列值的情况。（）
由于散列值的计算和指定索引访问数组元素所需要的时间都和数据的个数无关，所以散列表的访问计算量为o(1)。
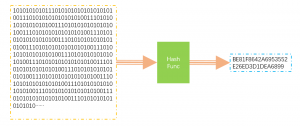
下图就是Hash函数的一个简单的说明，任意长度的数据通过HashFunc映射到一个较短的数据集中。

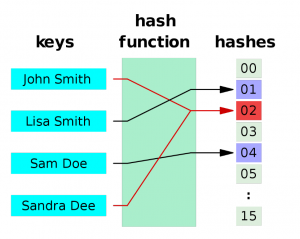
关于Hash碰撞，下图很清晰的就解释了，可从图中得知Sandra Dee和John Smith通过Hashfunc运算后都落在了02的位置,产生了碰撞和冲突。

常见的构造Hash函数的算法有以下几种。

1. 直接寻址法：取keyword或keyword的某个线性函数值为散列地址。即H(key)=key或H(key)= a*key+b,当中a和b是常数（这样的散列函数叫做自身函数）

2. 数字分析法：分析一组数据，比方一组员工的出生年月日，这时候我们发现出生年月日的前几位数字大体相同，这样话，出现冲突的几率就会非常大，可是我们发现年月日的后几位和详细日期的数字区分非常大，假设用后面的数字来构成散列地址，则冲突的几率会明显减少。因此数字分析法就是找出数字的规律，尽可能利用这些数据来构造冲突几率较低的散列地址。

3. 平方取中法：去keyword平方后的中间几位作为散列地址。

4. 折叠法：将keyword切割成位数同样的几部分，最后一部分位数能够不同，然后取这几部分的叠加值和（去除进位）作为散列地址。

5. 随机数法：选择一随机函数，取keyword的随机值作为散列地址，通常使用于keyword长度不同的场合。

6. 除留余数法：取keyword被某个不大于散列列表表长m的数p除后所得的余数为散列地址。即H(key) = key MOD p,p<=m,不仅能够对keyword直接取模，也可在折叠，平方取中等运算之后取模。对p的选择非常重要，一般取素数或m，若p选的不好，容易产生碰撞。

2，解决冲突算法

对于一个hash算法，不可避免会产生冲突，那么产生冲突以后如果处理，这是一个很关键的地方，目前常见的冲突解决算法有链地址法（chain-ing）,开放地址法（open addressing），再Hash法，公共溢出分区法，本文主要介绍链地址法（也就是c#的Dictionary所采用的），和开放地址法。

1. 链地址法

是将拥有相同散列值的元素存放在链表中，因此随着元素个数的增加，散列冲突和查询链表的时间也跟着增加，也就造成了性能的损失。优点：元素的删除可以用比较简单且搞性能的方式来实现。

2. 开放地址法

是在遇到冲突的时候，寻找一个新的数据存放空间（一般称为槽）。寻找空闲槽最简单的方法，就是循序遍历，直到找到空闲槽为止。
开放地址法中，在访问数据时候，如果散列值所代表的位置（槽）中不存在所希望的数据，则要么代表数据不存在，要么代表由于散列冲突而被转存到别的槽中了。于是通过以下算法来寻找目标槽位：

1. 计算数据（key）的散列值。
2. 从散列值找到相应的槽位（如果散列值比槽的数量大则取余数）
3. 如果槽位与数据一致，则使用该槽->查找结束。
4. 如果槽位为空闲，则散列表中不存在改数据->查找结束
5. 计算下一个槽的位置。
6. 返回第三步进行循环。

由于开放地址在数据存放上使用的是相对简单的数组方式，和链表相比较所需要的内存空间更小，因此在性能上存在有利的一面。
但是它的缺点也很明显，相比于原本的散列冲突发生的概率来说，它会让散列冲突发生的更加频繁。因此在这个方法里，会把有冲突的数据存放在下一个槽里，这就意味着下一个槽无法用来存放原本和散列值直接对应的数据。
当存放数据的数组逐渐被填满时，冲突的发生会十分频繁。当发生冲突以后，就必须通过计算来求得下一个槽的位置，用于槽查找的处理时间就会逐渐增加。因此，在开放地址法的设计中，所使用的数组大小必须是留有一定余量。
还有删除也是比较麻烦的，一般的元素和因冲突而不在原位的元素是混在一起的。因此无法简单地删除某个数据，要删除数据，仅仅将删除对象的数据所在槽置为空闲是不够的。
这样可能会把开放地址法中的连锁切断，从而导致本来存在的数据无法被找到。因此要删除数据，必须要将存放改元素的槽设置为一种特殊的状态，即“空闲（允许存放新数据）但不中断对下一个槽的计算”。

结论

随着散列表中存放的数据越来越多，发生冲突的危险性也随之增加。假设真有一种理想的散列函数，对于任何数据都能求出完全不同的散列值，那么当元素个数超过散列列表中槽的个数时，就不可避免地会产生冲突。尤其是开放地址法中当槽快要被填满时，所引发的冲突问题更加显著。
无论采用哪种方法，一旦发生冲突，就必须沿着某种连锁来寻找数据，因此无法实现o（1）的查找效率。
因此，在实用的散列表实现中，当冲突对查找效率产生的不利影响超过某一程度，就会对表的大小进行修改，从而努力在平均水平上保持o（1）的超早效率。
即便在最好的情况下，重组操作所需要的计算量也至少和元素的个数相关（即o（n）），不过，只要将重组的频率尽量控制在一个很小的值，就可以将散列表的平均访问消耗水平维持在o（1）。

三，Dictionary实现

Dictionary实现我们主要对着源码来解析，目前对照的版本为.NET Farmework 4.8，源码地址链接Dictionary
这一章主要介绍Dictionary中几个比较关键的类和对象，然后跟着代码来走一遍插入，删除和扩容的流程，相信大家就能理解它的设计原理。

1.Entry结构体

首先我们引入Entry这样一个结构体，它的定义如下代码所示。这是Dictionary类存放数据的最小单位，调用Add(Key,Value)方法添加的元素都会被封装在这样的一个结构体里。

private struct Entry{
    public int hashCode;        //哈希码的低31位，如果没有被使用则为-1
    public int next;            //下一个Entry元素的下标索引，如果没有下一个则为-1
    public TKey key;            //存放元素的key
    public TValue value;        //存放元素的value
}

2.其它关键私有变量

除了Entry结构体以外，还有几个关键的私有变量，其定义和解释如下代码所示：

private int[] buckets;                          //Hash桶
private Entry[] entries;                        //Entry数组，存放元素
private int count;                              //当前entries的index位置，当freeCount为0时启用
private int version;                            //当前版本，防止迭代过程中集合被更改
private int freeList;                           //被删除Entry在entries中的下标index，这个位置是空闲的
private int freeCount;                          //有多少个被删除的Entry，有多少个空闲的位置
private IEqualityComparer<TKey> comparer;     //比较器，并且为object生成Hashcode
private KeyCollection keys;                     // 存放key的集合
private ValueCollection values;                 //存放value的集合

上面代码中，需要注意的是buckets,entries这两个数组，这是实现Dictionary的关键。

3.Dictionary-Add操作

正常的Add操作

经过上面的分析，相信大家还是不是特别明白为啥需要这样的设计。现在让我们先走一遍Dictionary的Add流程，来体会一下。
首先我们用图的形容来描述一个Dictionary的数据结构，其中只画出了关键的地方。桶大小为4以及Entry大小也是4的一个数据结构。

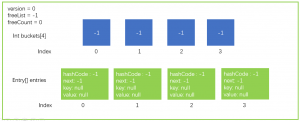
然后我们假设需要一个Add操作，dictionary.Add("a","b"),其中key = "a",value = "b".
大致的流程如下：

1. 根据key的值，计算出它的hashCode。我们假设“a”的hash值为6（comparer.GetHashCode(key)）.计算出来的hashCode和0x7FFFFFFF按位与（&）取底31位值，计算出的值为当前key的hashcode，假设为6。

2. 通过hashcode和buckets的长度去余，计算出改hashCode落在哪一个buckets桶中。现在桶的长度（buckets.Length）为4,那么假设取到的值为2（6%4）所以index的值就是2，也就是落在buckets[2]这个桶中。

3. 避开一种情况不谈，接下来它会将hashCode,key,value等信息存入entries[count]中，因为count位置是空闲的，所以值是可以放进去的；继续count++指向下一个空闲位置。上图中第一个位置，index = 0就是空闲，所以就存放在entries[0]的位置。

4. 将Entry的下标entryIndex赋值给buckets中对应下标bucket。步骤3中是存放在entries[0]的位置，所以buckets[2]=0。

5. 最后version++,集合发生了变化，所以版本需要+1.只有增加，替换和删除元素才会更新版本

实际步骤和上文的步骤会有些出入，现在这样区分只是为了能方便大家理解，后续将更详细的补充
完成上面Add操作后，数据结构更新成了下图这样的形式。

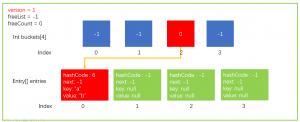
这样是理想情况下的操作，一个bucket中只有一个hashCode没有碰撞产生，但是实际上是会经常发生碰撞的；下面说下Dictionary类中是如果解决碰撞的。

碰撞的Add操作

我们继续执行一个Add操作，dictionary.Add("c","d"),假设根据上面的步骤1所得到的值还是6，那么求余数还是2，最后桶的index也还是2，按照以前的步骤执行完以后数据结构如下图所示

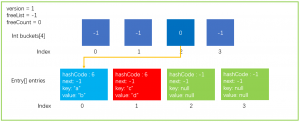
如果继续执行步骤4那么buckets[2] = 1,然后原来的buckets[2]=>entries[0]的关系就会丢失，这是我们不能接受的，所以在这个时候Entry中的next就开始发挥作用。
如果对应的buckets[index]有其它的元素已经存在，那么会执行以下两条语句，让新的entry.next指向之前的元素，让buckets[index]指向现在新的元素，就构成了一个单链表。

entries[index].next = buckets[targetBucket];
...
buckets[targetBucket] = index;

实际上步骤4也就是做一个这样的操作，并不会去判断是不是有其它元素，因为buckets中捅的初始值就是-1，所以直接赋值不会出现问题。
经过上面的步骤以后，数据结构就更新成了下面这个样子。

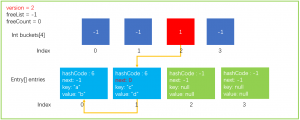
4.Dictionary-Find操作

为了方便演示如果查找，我们继续Add一个元素dictionary.Add("e","f"),comparer.GetHashCode("e")=7;7% buckets.Length=3,数据结构如下所示。

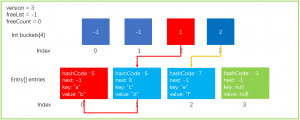
假设我们现在执行这样一条语句dictionary.GetValueOrDefault("a"),就会执行以下步骤

1. 获取key的hashCode，计算出所在的桶的位置。我们之前提到过，“a“的hashcode = 6，所以计算出来targetBucket=2。

2. 通过buckets[2]=1找到entries[1],比较key的值是否相等，相等就返回entryindex,不相等就继续entries[next]查找，直到找到key相等元素或者next==-1的时候，这里我们找到了key=="a"的元素，返回entryindex = 0.

3. 如果entryindex >= 0 那么返回对应的entries[entryindex]元素，否则返回default(TValue)。这里我们直接返回entries[0].value.
   整个查找过程如下图
   
   代码如下

   //寻找Entry元素的位置
   private int FindEntry(TKey key){
   if(key == null){
       ThrowHelper.ThrowArgumentNullException(ExceptionArgument.key);
   }
   if(buckets != null){
       int hashCode = comparer.GetHashCode(key)  & 0x7FFFFFFF; // 获取HashCode，忽略符号位
       // int i = buckets[hashCode % buckets.Length] 找到对应桶，然后获取entry在entries中位置
       // i >= 0; i = entries[i].next 遍历单链表
       for (int i = buckets[hashCode % buckets.Length]; i >= 0; i = entries[i].next) {
           // 找到就返回了
           if (entries[i].hashCode == hashCode && comparer.Equals(entries[i].key, key)) return i;
       }
   }
   return -1;
   }
   ...
   internal TValue GetValueOrDefault(TKey key){
   int i = FindEntry(key);
   // 大于等于0代表找到了元素位置，直接返回value
   // 否则返回该类型的默认值
   if (i >= 0) {
       return entries[i].value;
   }
   return default(TValue);
   }

   5.Dictionary-Remove操作

   前面介绍了增加，查找，接下来向大家介绍Dictionary是如何执行删除操作。我们沿用之前的Dictionary数据结构。
   
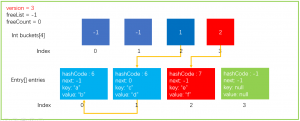
   删除前面的步骤和查找类似，也是需要找到元素的位置，然后再进行删除的操作。
   我们现在执行这样的一条语句dictionary.Remove("a")，hashFunc运算结果和上文中一致，步骤大部分与查找类似，我们直接看摘录的代码：

   public bool Remove(TKey key){
   if(key == null){
       ThrowHelper.ThrowArgumentNullException(ExceptionArgument.key);
   }
   if(buckets != null){
        // 1. 通过key获取hashCode
       int hashCode = comparer.GetHashCode(key) & 0x7FFFFFFF;
       // 2. 取余获取bucket位置
       int bucket = hashCode % buckets.Length;
       // last用于确定是否当前bucket的单链表中最后一个元素
       int last = -1;
         // 3. 遍历bucket对应的单链表
       for (int i = buckets[bucket]; i >= 0; last = i, i = entries[i].next) {
           if (entries[i].hashCode == hashCode && comparer.Equals(entries[i].key, key)) {
               // 4. 找到元素后，如果last< 0，代表当前是bucket中最后一个元素，那么直接让bucket内下标赋值为 entries[i].next即可
               if (last < 0) {
                   buckets[bucket] = entries[i].next;
               }
               else {
                   // 4.1 last不小于0，代表当前元素处于bucket单链表中间位置，需要将该元素的头结点和尾节点相连起来,防止链表中断
                   entries[last].next = entries[i].next;
               }
               // 5. 将Entry结构体内数据初始化
               entries[i].hashCode = -1;
               // 5.1 建立freeList单链表
               entries[i].next = freeList;
               entries[i].key = default(TKey);
               entries[i].value = default(TValue);
               // *6. 关键的代码，freeList等于当前的entry位置，下一次Add元素会优先Add到该位置
               freeList = i;
               freeCount++;
               // 7. 版本号+1
               version++;
               return true;
           }
       }
   }
   return false;
   }

   执行完上面代码后，数据结构就更新成了下图所示，需要注意的是version,freelist,freecount的值都被更新了。
   

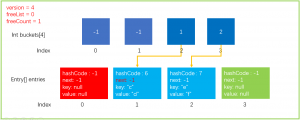
   6.Dictionary-Resize操作（扩容）

   有细心的小伙伴可能看过了Add的操作以后就会想了，buckets,entries不就是两个数组嘛，万一数组被放满了那怎么办？接下来就是我要说的Resize（扩容）这种操作了，对我们的buckets,entries进行扩容。

   6.1扩容操作的触发条件

   首先我们需要知道在什么情况下，会发生扩容操作：第一种情况自然就是数组已经满了，没有办法继续存放新的元素。如下所示
   
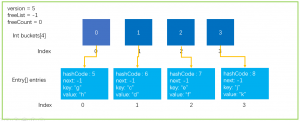
   从上文中大家也知道了，Hash运算会不可避免的产生冲突，Dictionary中使用链地址法来解决冲突的问题，但是如果一直都在冲突那就会如下所示：
   
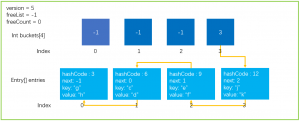
   所有的元素都刚好落在了buckets[3]上面，结果就是导致了时间复杂度0（n）,查找性能就会下降；所以第二种，Dictionary中发生碰撞的次数太多，导致严重的性能问题，也会触发扩容操作。
   **目前.Net Framwork 4.8中设置的碰撞次数阈值为100.

   public const int HashCollisionThreshold = 100;

   6.2扩容操作如何进行

   为了给大家演示清楚，模拟了以下的这种数据结构，大小为2的Dictionary，假设碰撞的阈值为2；现在触发Hash碰撞扩容
   
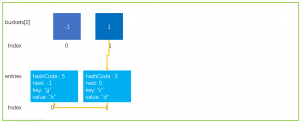
   开始扩容操作

4. 申请两倍于现在大小的buckets，entries

5. 将现有的元素拷贝到新的entries

完成上面的两步操作后，新的数据结构如下图所示。

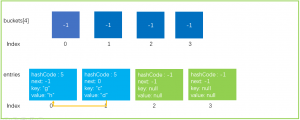
3. 如果是Hash碰撞扩容，使用新的HashCode函数来重新计算hash值

上文提到了，这是发生了Hash碰撞扩容，所以需要使用新的Hash函数计算Hash值，新的Hash函数并不一定能解决碰撞的问题，可能还会更糟糕，像下图中一样还是会落在同一个bucket
上。

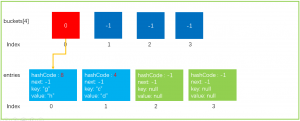
4. 对entries每个元素bucket=newEntries[i].hashCode%newSize确定新的buckets位置

5. 重建hash链，newEntries[i].next=buckets[bucket];buckets[bucket]=i;

因为buckets也扩容了两倍大小，所以需要重新确定hashCode在哪个bucket中；最后重新建立hash单链表。

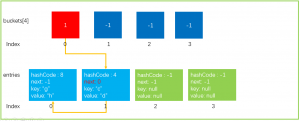
这就完成了扩容的操作，如果是达到Hash碰撞阈值触发的扩容可能扩容后结果会更差。
在JDK中，HashMap如果碰撞的次数太多了，那么会将单链表转换为红黑树提升查找性能，目前在.Net Framwork中还没有这样的优化，.Net Core中已经有了类似的优化。
每次扩容操作都需要遍历所有元素，会影响性能。所以创建Dictionary实例时最好设置一个预估的初始大小。

private void Resize(int newSize,bool forceNewHashCodes){
    Contract.Assert(newSize >= entries.Length);
    //1.申请新的Buckets和entries
    int[] newBuckets = new int[newSize];
    for(int i = 0;i<newBuckets.Length;i++) newBuckets[i] = -1;
    Entry[] newEntries = new Entry[newSize];
    //2.将entries内元素拷贝到新的entries内
    Array.Copy(entries,0,newEntries,0,count);
    //3.如果是Hash碰撞扩容，使用新的HashCode函数重新计算Hash值
    if(forceNewHashCodes){
        for(int i = 0; i<count; i++){
            if(newEntries[i].hashCode != -1){
                newEntries[i].hashCode = (comparer.GetHashCode(newEntries[i].key) & 0x7FFFFFFF);
            }
        }
    }
    //4.确定新的bucket位置
    //5.重建Hash单链表
    for(int i = 0;i < count; i++){
        if(newEntries[i].hashCode >= 0){
            int bucket = newEntries[i].hashCode % newSize;
            newEntries[i].next = newBuckets[bucket];
            newBuckets[bucket] = i;
        }
    }
    buckets = newBuckets;
    entries = newEntries;
}

Dictionary-再谈Add操作

在我们之前的Add操作步骤中，提到了这样的一句话，这里提到会有一种其它的情况，那就是有元素被删除的情况。

1. 避开一种其它情况不谈，接下来它会将hashCode,key,value等信息存入entries[count]中，因为count位置是空闲的；继续count++指向下一个空闲位置。上图中第一个位置，index=0就是空闲位置，所以就存在entries[0]的位置。

因为count是通过自增的方式来指向entries[]下一个空闲的entry，如果有元素被删除了，那么在count之前的位置就会出现一个空闲的entry位置，代码如下：

private void Insert(TKey key,TValue value,bool add){
    if(key == null){
        ThrowHelper.ThrowArgumentNullException(ExceptionArgument.key);
    }
    if(buckets == null)Initialize(0);
    //通过key获得hashCode
    int hashCode = comparer.GetHashCode(key) & 0x7FFFFFFF;
    //计算出目标bucket下标
    int targetBucket = hashCode%buckets.Length;
#if FEATURE_RANDOMIZED_STRING_HASHING
    //碰撞次数
    int collisionCount = 0;
#endif
    for(int i = buckets[targetBucket];i>= 0;i = entries[i].next){
        if(entries[i].hashCode == hashCode&&comparer.Equals(entries[i].key,key)){
            //如果增加操作，遍历到相同的元素，那么抛出异常
            if(add){
                ThrowHelper.ThrowArgumentException(ExceptionResource.Argument_AddingDuplicate);
            }
            //如果不是增加操作，那可能是索引赋值操作
            //赋值成功版本加一后退出
            entries[i].value = value;
            version++;
            return;
        }
#if FEATURE_RANDOMIZED_STRING_HASHING
        //遍历一次元素，都是一次碰撞
        collisionCount++;
#endif  
    }
    int index;
    //如果有被删除的元素，那么将元素放在被删除元素的空闲位置
    if(freeCount > 0){
        index = freeList;
        freeList = entries[index].next;
        freeCount--;
    }else{
        //如果当前的entries已满，那么出发扩容
        if(count == entries.Length){
            Resize();
            targetBucket = hashCode%buckets.Length;
        }
        index = count;
        count++;
    }
    //给entry赋值
    entries[index].hashCode = hashCode;
    entries[index].next = buckets[targetBucket];
    entries[index].key = key;
    entries[index].value = value;
    buckets[targetBucket] = index;
    //版本号加一
    version++;
    #if FEATURE_RANDOMIZED_STRING_HASHING
#if FEATURE_CORECLR
            // In case we hit the collision threshold we'll need to switch to the comparer which is using randomized string hashing
            // in this case will be EqualityComparer<string>.Default.
            // Note, randomized string hashing is turned on by default on coreclr so EqualityComparer<string>.Default will 
            // be using randomized string hashing
            //如果碰撞次数大于设置的最大碰撞次数，那么出发hash碰撞扩容
            if (collisionCount > HashHelpers.HashCollisionThreshold && comparer == NonRandomizedStringEqualityComparer.Default)
            {
                comparer = (IEqualityComparer<TKey>) EqualityComparer<string>.Default;
                Resize(entries.Length, true);
            }
#else
            if(collisionCount > HashHelpers.HashCollisionThreshold && HashHelpers.IsWellKnownEqualityComparer(comparer))
            {
                comparer = (IEqualityComparer<TKey>) HashHelpers.GetRandomizedEqualityComparer(comparer);
                Resize(entries.Length, true);
            }
#endif // FEATURE_CORECLR

#endif
}

现在在看完整的Add代码，是不是很简单了。

8.Collection版本控制

在上文中提到过一个version这个变量，在每一次增加，修改，删除的时候，都会对这个变量做一次递增；那么这个变量存在的意义是什么呢？
首先来看一段代码的运行，先实例化一个Dictionary的实例，然后通过foreach来遍历该实例，在foreach的代码块中使用remove(key)来删除元素

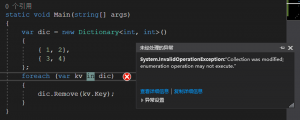
结果就是抛出来System.InvalidOperationException:"Collection was modified...这样的异常，迭代过程中不允许集合出现变化。这个就是用version来实现版本控制。
我们开看下源码是怎么实现版本控制的

[Serializable]
public struct Enumerator: IEnumerator<KeyValuePair<TKey,TValue>>,IDictionaryEnumerator{
    private Dictionary<TKey,TValue> dictionary;
    private int version;
    private int index;
    internal Enumerator(Dictionary<TKey,TValue> dictionary, int getEnumeratorRetType) {
        this.dictionary = dictionary;
        //这个给版本号赋值
        version = dictionary.version;
        index = 0;
        this.getEnumeratorRetType = getEnumeratorRetType;
        current = new KeyValuePair<TKey, TValue>();
    }
    public bool MoveNext() {
        //这里看版本是否有修改
        if (version != dictionary.version) {
            ThrowHelper.ThrowInvalidOperationException(ExceptionResource.InvalidOperation_EnumFailedVersion);
        }
    }
}

所以在迭代开始的时候记录一下version，后续在每一次迭代过程中都会去检查。